The Arithmetic and Geometric Means
You’re probably familiar with the arithmetic mean, which is most people mean (heh) when they say “average”:
$$\displaystyle A(x_i) = \frac{1}{n}\sum_i x_i $$
where $x_i$ is a set of $n$ real numbers. The arithmetic mean answers the question “If all these numbers were equal, what would they have to be to add to a given sum?”. There is also the geometric mean:
$$\displaystyle G(x_i) = \left( \prod_i x_i \right)^\frac{1}{n} $$
which answers the question “If all these numbers were equal, what would they have to be to multiply to a given product?”. It turns out that the geometric mean is always less than or equal to the arithmetic:
$$\displaystyle G(x_i) \le A(x_i) $$
which I think is not obvious from the definitions. But with some manipulations we can show that this inequality arises because the exponential function $e^x$ is concave up.
Since the geometric mean involves a root extraction, it is not defined if the product inside is negative (we insist on getting a real-valued from a set of real numbers $x_i$). We’re also uninterested in the case where one of the $x_i$ is zero, which would cause the product and therefore the geometric mean to be zero. So for the sake of the present discussion we can assume $x_i >0$ which allows us to write $x_i = e^{\xi_i}$ where each $\xi_i$ is some real number, possibly negative. Then the geometric mean can be written as:
$$\displaystyle G(x_i) = \left( \prod_i e^{\xi_i} \right)^\frac{1}{n} = \left(\exp\left(\sum_i \xi_i\right)\right)^{\frac{1}{n}} = \exp\left(\frac{1}{n}\sum_i \xi_i\right) = \exp(A(\xi_i)) $$
So we can write $G$ as:
$$\displaystyle G(x_i) = T(A(T^{-1}(x_i))) $$
where the function $T$ is the exponential function, $T(x) = e^{x} = \exp(x)$. We have that $x_i = T(\xi_i)$, so we may also write:
$$\displaystyle G(T(\xi_i)) = T(A(T^{-1}(x_i))) = T(A(T^{-1}(T(\xi_i)))) = T(A(\xi_i))$$
In other words, $G\circ T = T\circ A$. $T(x) = e^x$ is concave up:
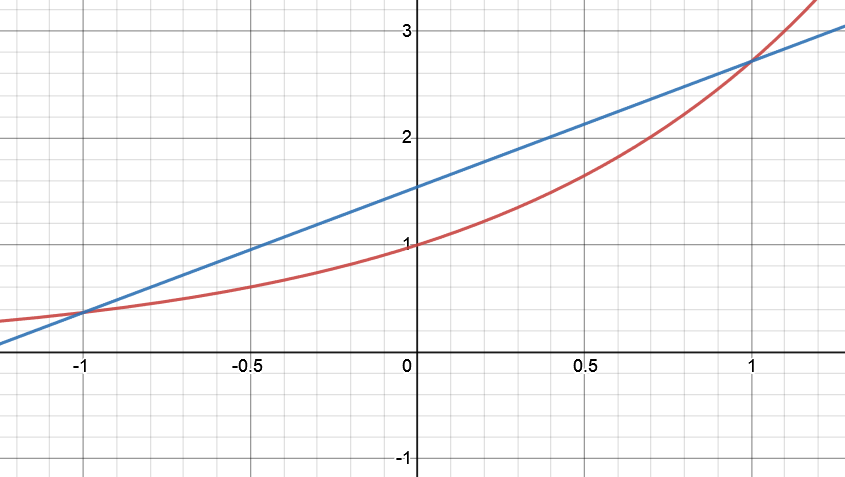
Mathematically, this means that for any $a$ and $b$, and any $0 \le \theta \le 1$:
$$\displaystyle T((1-\theta)a +\theta b) \le (1-\theta) T(a) + \theta T(b) $$
By applying this fact recursively, one can show that it implies:
$$\displaystyle T(A(x_i)) \le A(T(x_i)) $$
which, when substituted into the rewritten geometric mean, gives us the expected inequality:
$$\displaystyle G(T(\xi_i)) = T(A(\xi_i)) \le A(T(\xi_i)) \Leftrightarrow G(x_i) \le A(x_i)$$
By Any Other Means
The geometric mean is essentially defined by the choice of $T(x) = e^x$ in the relation $G(x_i) = T(A(T^{-1}(x_i)))$. We can obtain other means by choosing different functions for $T$, and the argument in the preceding section guarantees that any of those means will also be less than or equal to the arithmetic mean if the chosen $T$ is concave up.
$$\displaystyle M(x_i) = T(A(T^{-1}(x_i))) \le A(x_i),\,\,T\text{ concave up} $$
A similar argument with the inequality reversed applies when $T$ is concave down:
$$\displaystyle M(x_i) = T(A(T^{-1}(x_i))) \ge A(x_i),\,\,T\text{ concave down} $$
For example, the harmonic mean arises from choosing $T(x) = 1/x$:
$$\displaystyle H(x_i) = T(A(T^{-1}(x_i))) =\frac{1}{\frac{1}{n}\sum_i \frac{1}{x_i}} $$
$1/x$ is concave up, so $H(x_i) \le A(x_i)$. Similarly, one might concoct a “reverse geometric” mean by using $T(x) = \ln x$, which is concave down, in place of $T(x) = e^x$ in the definition of the geometric mean:
$$\displaystyle R(x_i) = \ln\left(\frac{1}{n}\sum_i e^{x_i}\right) $$
which would exceed the arithmetic mean, $R(x_i) \ge A(x_i)$. Any monotone function that is concave up over its domain or concave down over its domain induces its own type of mean.
Living Within One’s Means
So far we have established relationships between uncommon means and the arithmetic mean. Can we relate other means directly? For example, it is a fact that the harmonic mean is bounded by the geometric mean, $H(x_i) \le G(x_i)$. At the moment we only know that $H(x_i) \le A(x_i)$ and $G(x_i) \le A(x_i)$. Can we derive this fact within the framework we have established? Of course we can.
Let $T_1$ and $T_2$ be two monotone functions which do not change their concavity, meaning they induce their own means $M_1$ and $M_2$ respectively:
$$\displaystyle \begin{aligned} M_1(x_i) &= T_1(A(T_1^{-1}(x_i))) \\ M_2(x_i) &= T_2(A(T_2^{-1}(x_i))) \end{aligned}$$
Define $\xi_i$ by $x_i = T_1(\xi_i)$. Then the two means become:
$$\displaystyle \begin{aligned} M_1(x_i) &= T_1(A(\xi_i)) \\ M_2(x_i) &= T_2(A(T_2^{-1}(T_1(\xi_i)))) \end{aligned}$$
Without loss of generality, suppose $M_1\le M_2$. Then:
$$\displaystyle T_1(A(\xi_i)) \le T_2(A(T_2^{-1}(T_1(\xi_i)))) $$
If $T_2^{-1}$ increases monotonically, we may apply it to both sides without reversing the inequality:
$$\displaystyle T_2^{-1}(T_1(A(\xi_i))) \le A(T_2^{-1}(T_1(\xi_i))) $$
But this is just $T(A(\xi_i)) \le A(T(\xi_i))$ with $T = T_2^{-1}\circ T_1$, and we already know that that inequality holds when $T$ is concave up. Putting it all together, we have that:
$$\displaystyle \begin{aligned} &M_1(x_i) = T_1(A(T^{-1}_1(x_i))) \le T_2(A(T^{-1}_2(x_i))) = M_2(x_i) \\ &T_2^{-1}\text{ monotone increasing and } T_2^{-1}\circ T_1 \text{ concave up}\end{aligned}$$
Choosing $T_1(x) = 1/x$ for the harmonic mean and $T_2(x) = e^x$ for the geometric, we find that $T_2^{-1}(x) = \ln x$ is monotonically increasing and $T_2^{-1}\circ T_1 = \ln(1/x) = -\ln(x)$ is concave up, so $H(x_i) \le G(x_i)$. Note that swapping $T_1$ and $T_2$ in this case does not work, because $T_2^{-1} = 1/x$ is monotone decreasing.
The Ends Justify the Means
And that’s a wrap. Go concoct some means and find the inequalities relating them. I mean it!