You know about electricity, and you know about magnetism, and you’ve probably heard the word “electromagnetism” somewhere before to refer to electricity and magnetism combined in some sense. But why do these two seemingly different phenomena get lumped together into one word, whereas there’s no such thing (yet?) as “electrogravity”? If you know some more physics than the everyday person, you might know that magnetic fields are created by moving electrical charges such as the electric current in a wire, which is just electrons moving through the metal. And you might also know that a changing magnetic field will cause an electric current in a wire placed in that field. So there is clearly some linkage between electricity and magnetism. But why is there one?
The Physics
Believe it or not, it’s because of relativity! Imagine a setup with a current flowing (i.e. electrons moving) through an infinite wire with a small charged object, say, an alpha particle, moving parallel to the wire:
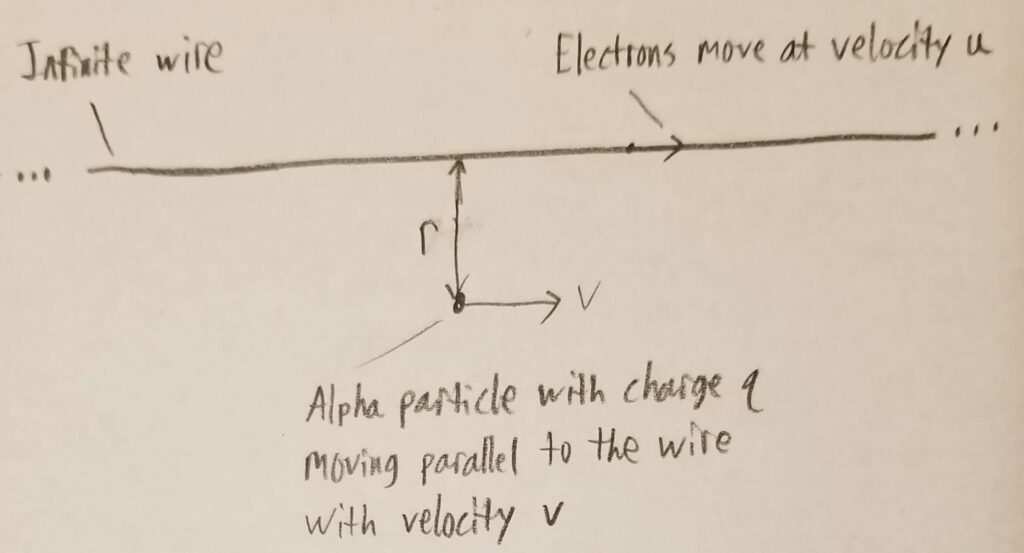
The protons in the wire do not flow like the electrons (they’re confined in the nuclei of the atoms comprising the wire), so we can regard them as stationary. So our alpha particle moves at velocity $v$ relative to the protons, but with velocity $v-u$ relative to the electrons. If you imagine yourself sitting on the alpha particle, it would appear to you that the electrons in the wire were moving at a different velocity than the protons in the wire.
Relativity implies that an observer measuring the length of a moving object will measure that object as being shorter than what would be measured if he were moving along with the object. This phenomenon is called “length contraction”. Since this blog is a math blog, not a physics blog, you’ll just have to take my word for it on this one. For present purposes, what matters here is that our alpha particle will see the average spacing between electrons as differing from the average spacing between protons in the wire because the two sets of particles are moving at different speeds relative to the alpha particle. Thus to the alpha particle, the wire appears to have a net charge which will cause a force on the alpha particle (since opposite charges attract and like ones repel each other). But to an outside observer, the alpha particle appears to be subjected to a strange force from the wire — we call this force magnetism.
The Math
We will derive the magnetic field caused by an infinite wire carrying a current using the above train of thought and Coulomb’s law for the electrostatic force $F_C$ between two point charges:
$$\displaystyle F_C = \frac{kq_1 q_2}{d^2} $$
where $k$ is a physical constant, $q_1$ and $q_2$ are the electric charges of the two point objects, and $d$ is the distance between them. First we need to know the force on our alpha particle due to a uniform charge distribution along the whole infinite wire. Let $\rho$ be the charge per unit length in the wire. Then the
$$\displaystyle F = \int_{-\infty}^\infty \frac{k\rho q}{x^2 + r^2}\frac{r}{\sqrt{x^2+r^2}}\,dx = \frac{kq\rho}{r^2}\int_{-\infty}^{\infty} \frac{1}{\left( 1 + \frac{x^2}{r^2} \right)^\frac32}\,dx $$
This integral may look nasty, but becomes quite easy after the substitution $\frac{x}{r} = \tan{\theta}$, from which follows that $dx = r\sec^2{\theta}d\theta$.
$$\displaystyle F = \frac{kq\rho}{r}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\sec^2\theta}{\sec^3\theta} \,d\theta = \frac{kq\rho}{r}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos\theta \,d\theta = \frac{2kq\rho}{r} $$
We will use this expression to compute the force from the distributions of positive and negative charges in the wire as experienced by the alpha particle. The alpha particle will see a density $\rho^+$ of positive charges and a density $-\rho^-$ of negative charges, which are related by:
$$\displaystyle 1 = \frac{\rho^- L^-}{\rho^+ L^+} = \frac{\rho^-}{\rho^+} \frac{L^-}{L} \frac{L}{L^+} $$
where $L$ is the average separation between positive charges as measured by an observer not moving with respect to those charges (note that we are taking $\rho^+$ and $\rho^-$ to be positive). From relativity we have:
$$\displaystyle \frac{L^-}{L} = \sqrt{1 – \left( \frac{v-u}{c} \right)^2} \,\,\, \frac{L^+}{L} = \sqrt{1 – \left( \frac{v}{c} \right)^2} $$
where $c$ is the speed of light. Plugging these back in:
$$\displaystyle 1 = \frac{\rho^-}{\rho^+} \sqrt{\frac{1 – \left( \frac{v-u}{c} \right)^2}{1 – \left( \frac{v}{c} \right)^2}} \Rightarrow \frac{\rho^+}{\rho^-} = \sqrt{\frac{1 – \left( \frac{v-u}{c} \right)^2}{1 – \left( \frac{v}{c} \right)^2}} $$
So we can write the force on the alpha particle from the wire as:
$$\displaystyle F = \frac{2kq\rho^+}{r} – \frac{2kq\rho^-}{r} = \frac{2kq\rho^-}{r} \left( \frac{\rho^+}{\rho^-} – 1 \right) $$
This formula won’t look familiar, but since the velocity $v$ of the alpha particle and especially $u$, the velocity of the electrons in the wire, are exceedingly tiny compared with the speed of light, we can replace $\frac{\rho^+}{\rho^-} – 1$ by an approximation that will be good for all everyday practical purposes (not that one encounters many infinite wires in practice). Observe that:
$$\displaystyle \ln\left( \frac{\rho^+}{\rho^-} \right) = \frac12\ln\left( 1 – \left( \frac{v-u}{c} \right)^2 \right) – \frac12\ln\left( 1 – \left( \frac{v}{c} \right)^2 \right) $$
Since $u$ is extremely tiny, we may approximate this expression by the derivative of a related function:
$$\displaystyle \begin{aligned} \ln\left( \frac{\rho^+}{\rho^-} \right) &\approx -u\frac{d}{dx} \left[ \frac12\ln\left( 1 – \left(\frac{x}{c}\right)^2 \right) \right]\Bigg|_{x=v} \\ &= -\frac{u}{2}\frac{1}{1 – \left(\frac{v}{c}\right)^2}\cdot\frac{-2}{c}\frac{v}{c} \\ &= \frac{u}{c}\frac{v}{c}\frac{1}{1-\left(\frac{v}{c}\right)^2} \end{aligned}$$
Again since $u/c$ and $v/c$ are small, it follows that:
$$\displaystyle \frac{\rho^+}{\rho^-} – 1 = e^{\ln\left(\frac{\rho^+}{\rho^-}\right)} – 1 \approx \ln\left(\frac{\rho^+}{\rho^-}\right) \approx \frac{u}{c}\frac{v}{c}\frac{1}{1-\left(\frac{v}{c}\right)^2} $$
So we may very accurately approximate the force from the wire as:
$$\displaystyle \begin{aligned} F &\approx \frac{2kq\rho^-}{r}\frac{u}{c}\frac{v}{c}\frac{1}{1-\left(\frac{v}{c}\right)^2} \\ &\approx \frac{2kq\rho^-}{r}\frac{u}{c}\frac{v}{c} \end{aligned}$$
making use of the fact that $\frac{1}{\left(1-(\frac{v}{c})^2\right)}$ will be essentially $1$ since $\frac{v}{c}$ is tiny. Now $\rho^-$ is the density of negative charges and $u$ is their velocity, so the product $u\rho^-$ is the current $I$ flowing in the wire. So we end up with our final expression for the force on the alpha particle:
$$\displaystyle F = \frac{2kIv}{c^2 r} $$
Put another way, the strength $B$ of the magnetic field created by the wire’s current is:
$$\displaystyle B = \frac{2kI}{c^2 r} $$
Compare this to the textbook expression for the magnetic field:
$$\displaystyle B_{textbook} = \frac{\mu_0 I}{2\pi r} $$
we see some similarities, but the latter is phrased in terms of the magnetic permeability $\mu_0$ and has $\pi$. But, it turns out that:
$$\displaystyle k = \frac{1}{4\pi\epsilon_0}$$
and
$$\displaystyle c^2 = \frac{1}{\epsilon_0\mu_0}$$
where $\epsilon_0$ is the electric permittivity. Plugging in these facts we find that the two expressions for the force are, no surprise, equal:
$$\displaystyle \begin{aligned} B = \frac{2kI}{c^2 r} &= \frac{2}{c^2}\frac{1}{4\pi\epsilon_0}\frac{I}{r} \\ &= 2\epsilon_0\mu_0\frac{1}{4\pi\epsilon_0}\frac{I}{r} \\ &= \frac{\mu_0 I}{2\pi r} \end{aligned}$$.
The Aftermath
We have shown that what we think of as magnetism is actually just electrostatic attraction/repulsion acting under relativity. The effects of relativity are usually only detectable by us as very slight deviations in the ticking of ultra-precise atomic clocks traveling at what we consider high speeds, but which are still much less than the speed of light. In contrast, electrons in wires move hardly at all. But since there are so many electrons in the wire, the infinitesimal speed they do have is enough to make relativity detectable in everyday life as magnetism.