A cyclic quadrilateral is a four-sided polygon whose vertices all lie on a circle, like this one:
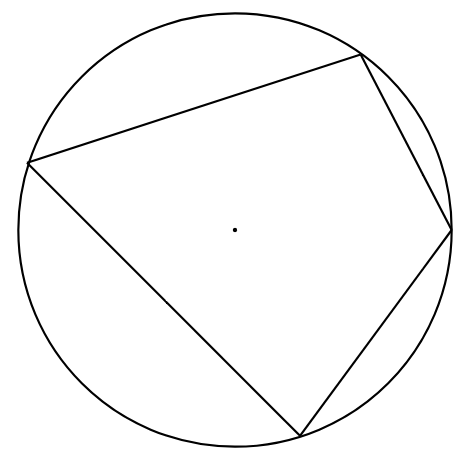
The center of this circle (the “circumscribed circle” or “circumcircle”) is called the “circumcenter”, marked by a dot in the above figure.
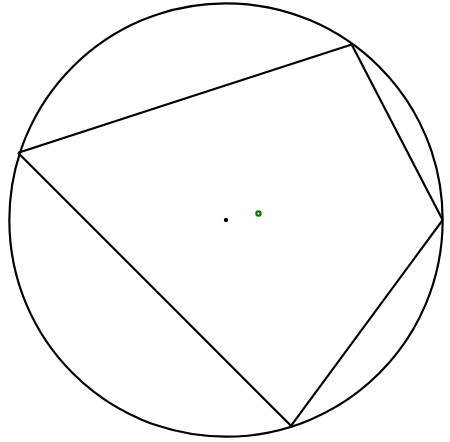
Quadrilaterals have many special points that get called centers, such as the circumcenter, but the most commonsensical one is the centroid. The centroid is the center of gravity that the quadrilateral would have if it were a thin plate of some material with uniform density. In other words, it is the balance point. Below is the same figure with the centroid marked in green. Clearly the centroid and the circumcenter are not the same point, and indeed most of the time, all the different centers are different – but not always. When are the centroid and circumcenter of a cyclic quadrilateral the same point?
Consider the circumcenter to be at the origin. Locate the i-th vertex by the vector $\vec{r}_i$, numbered in sequence counterclockwise around the circle, and split the quadrilateral into triangles formed by vertices 1-2-3 and vertices 3-4-1. The centroid of a triangle is simply the average of its vertices, and the centroid of the whole quadrilateral lies on the line segment connecting the centroids of these two triangles.
Without loss of generality, assume that the centroid $\vec{c}_2$ of Triangle 1-2-3 has an $x$ coordinate of zero. Then for the circumcenter to have any chance of being the centroid it needs to lie on the line between $\vec{c}_2$ and $\vec{c}_4$, the centroid of Triangle 3-4-1, for which $\vec{c}_4$ must also have zero $x$ coordinate. Now returning to the general case, the $x$ coordinate is the component in the direction normal to $\vec{c}_2$. That is, letting $\vec{z}$ be a unit vector pointing out of the page:
$$\displaystyle \vec{c}_4\cdot(\hat{z}\times\vec{c}_2) = 0$$
This is a scalar triple product. Trivially, we can also write:
$$\displaystyle \vec{c}_2\cdot(\hat{z}\times\vec{c}_2) = 0$$
Subtracting the two:
$$\displaystyle (\vec{c}_4-\vec{c}_2)\cdot(\hat{z}\times\vec{c}_2) = 0$$
Now using the fact that the centroids are the averages of their respective triangles:
$$\displaystyle (\vec{r}_4 – \vec{r}_2)\cdot(\hat{z}\times(\vec{r}_1 + \vec{r}_2 + \vec{r}_3)) = 0$$
where needless multiplicative factors have been dropped since the right-hand side is zero. Also for that reason, we can rearrange the triple product to obtain:
$$\displaystyle (\hat{z}\times(\vec{r}_4 – \vec{r}_2))\cdot(\vec{r}_1 + \vec{r}_2 + \vec{r}_3) = 0$$
The $\hat{z}\times(\vec{r}_4 – \vec{r}_2)$ could be replaced by a vector of any length that is perpendicular to $\vec{r}_4 – \vec{r}_2$. Since the $\vec{r}_i$ all have the same length due to the quadrilateral being cyclic, we have:
$$\displaystyle (\vec{r}_i – \vec{r}_j)\cdot(\vec{r}_i + \vec{r}_j) = \vec{r}_i\cdot\vec{r}_i – \vec{r}_j\cdot\vec{r}_j = 0 $$
So $\vec{r}_4 + \vec{r}_2$ will serve as the normal vector we want:
$$\displaystyle (\vec{r}_4 + \vec{r}_2)\cdot(\vec{r}_1 + \vec{r}_2 + \vec{r}_3) = 0 $$
Expanding the dot product:
$$\displaystyle (\vec{r}_2 + \vec{r}_4)\cdot(\vec{r}_1 + \vec{r}_3) + (\vec{r}_2 + \vec{r}_4)\cdot\vec{r}_2 =0 $$
We could also have divided the quadrilateral into triangles 2-3-4 and 4-1-2, for which the same process eventually gives:
$$\displaystyle (\vec{r}_3 + \vec{r}_1)\cdot(\vec{r}_2 + \vec{r}_4 + \vec{r}_3) = 0 $$
$$\displaystyle (\vec{r}_1 + \vec{r}_3)\cdot(\vec{r}_2 + \vec{r}_4) + (\vec{r}_1 + \vec{r}_3)\cdot\vec{r}_3 =0 $$
Equating the two expanded versions and using the fact that $\vec{r}_3\cdot\vec{r}_3 = \vec{r}_2\cdot\vec{r}_2$ because the quadrilateral is cyclic, we obtain:
$$\displaystyle \vec{r}_1\cdot\vec{r}_3 = \vec{r}_2\cdot\vec{r}_4 $$
Since the lengths of the $\vec{r}_i$ are all equal, this last equation implies that the angle from point 1 to point 3 matches the angle from point 2 to point 4. Equivalently, the diagonal of the quadrilateral from point 1 to point 3 has the same length as that from point 2 to point 4. This fact narrows the search for quadrilaterals down to trapezoids (which include squares and rectangles as special cases). Consider a trapezoid as shown below.
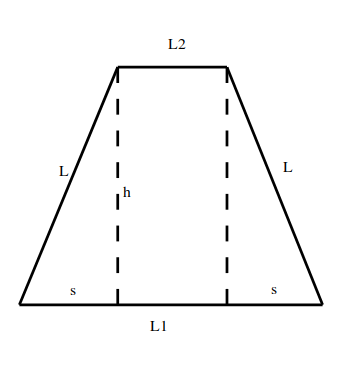
$L_1$ is the length of the lower edge, $L_2$ that of the upper, and $h$ the height. For this trapezoid to be cyclic, the perpendicular bisectors of the four edges must all meet at a point. Since the vertical centerline is such a bisector, it is enough to find its intersection with the bisector of one of the slant edges. Some algebra shows that that intersection occurs at a height $y_{circ}$ above the base:
$$\displaystyle y_{circ} = \frac{h}{2} – \frac{s}{h}\left( \frac{L_1-s}{2} \right) $$
On the other hand, the centroid of the trapezoid can be found from those of the two triangular pieces and the central rectangle:
$$\displaystyle y_{centroid} = \frac{2\frac{hs}{2}\frac{h}{3} + hL_2\frac{h}{2}}{hs+hL_2} = \frac{\frac{hs}{3} + \frac{h}{2}L_2}{L_1 – s} $$
We want to know when these two heights match:
$$\displaystyle \frac{h}{2} – \frac{s}{h}\left( \frac{L_1-s}{2} \right) = \frac{\frac{hs}{3} + \frac{h}{2}L_2}{L_1 – s} $$
$$\displaystyle \frac{h}{2} – \frac{s}{h}\left( \frac{L_1+L_2}{4} \right) = \frac{\frac{2hs}{3} + hL_2}{L_1 + L_2} $$
$$\displaystyle \frac{L_1+L_2}{2} – s\left(\frac{L_1+L_2}{2h}\right)^2 = L_2 + \frac{2s}{3}$$
$$\displaystyle \frac{L_1 – L_2}{2} – \frac{L_1-L_2}{2}\left(\frac{L_1+L_2}{2h}\right)^2 = \frac{L_1-L_2}{3}$$
At this point we can see that $L_1 = L_2$ implies that the centroid matches the circumcenter. This corresponds to the case where the trapezoid is actually a rectangle or square. Continuing, dividing through by $(L_1-L_2)/2$:
$$\displaystyle 1 – \left(\frac{L_1+L_2}{2h}\right)^2 = \frac{2}{3} $$
$$\displaystyle \frac{1}{3} = \left(\frac{L_1+L_2}{2h}\right)^2 $$
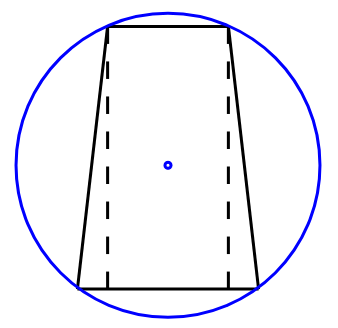
This is the criterion we want. Here is an example with $L_1 = 1.2$, $L_2 = 0.8$, $h = \sqrt{3}$: