1. Introduction
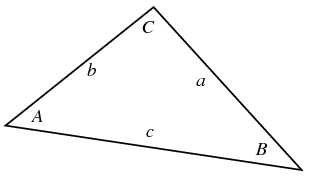
One might remember from high-school precalculus class something called the Law of Sines, and might even remember what it is because it has a memorable pattern:
$ \displaystyle \frac{\sin{A}}{a} = \frac{\sin{B}}{b} = \frac{\sin{C}}{c} \ \ \ \ \ (1)$
where $a$, $b$, and $c$ (lowercase) are the side lengths and $A$, $B$, and $C$ (uppercase) are the angles of a triangle opposite the sides with the corresponding letter.
One way to see the reason for (1) is to calculate the area ${V}$ of the triangle using the formula:
$ \displaystyle V = \frac{1}{2} ab\sin{C} \ \ \ \ \ (2)$
This formula asks you to pick an angle, then uses the lengths of the two sides forming the angle. Obviously the triangle’s area won’t depend on which angle you pick, so the areas you get using each choice will all match.
$ \displaystyle \begin{aligned} V = \frac{1}{2} ab\sin{C} &= \frac{1}{2} ac\sin{B} &= \frac{1}{2} bc\sin{A} \\ ab\sin{C} &= ac\sin{B} &= bc\sin{A} \\ abc\frac{\sin{C}}{c} &= abc\frac{\sin{B}}{b} &= abc\frac{\sin{A}}{a} \\ \end{aligned} \ \ \ \ \ (3)$
Then cancelling the common factor ${abc}$ gives you the Law of Sines, (1). That’s basically all that high school precalculus has to say on the matter because that class only deals with 2-dimensional shapes. In the wider world one might encounter a tetrahedron (plural: tetrahedra) which is the 3-dimensional analog of the triangle. Observe that:
- A triangle consists of 3 vertices that don’t all lie on the same line.
- Every vertex is connected to every other vertex.
However:
- A tetrahedron consists of 4 vertices that don’t all lie on the same plane.
- Every vertex is connected to every other vertex.
Because we added a dimension, we add an additional point and make the restriction about planes instead of lines, but the essence is the same. In fact, triangles and tetrahedra are the 2- and 3-dimensional cases of a simplex, which extends the idea to any number of dimensions.
If tetrahedra are the 3D versions of triangles, is there something like the Law of Sines for tetrahedra?
2. Notation
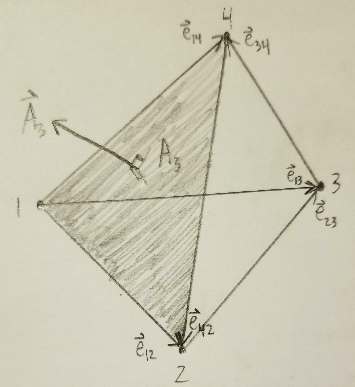
In the introduction I used $ {a}$,$ {b}$,$ {c}$ for side lengths and $ {A}$, $ {B}$, $ {C}$ for angles to match how the Law of Sines is commonly written in American high school books. But that system would be cumbersome and confusing for the explorations to follow. Instead, number the vertices of a tetrahedron like so:
- Face $ {i}$ is the face opposite vertex $ {i}$, which has area $ {A_i}$
- $ {\vec{e}_{ij}}$ is the vector from vertex $ {i}$ to vertex $ {j}$, and $ {e_{ij}}$ is its length
- $ {\vec{A}_i}$ is the vector with length $ {A_i}$, which is perpendicular to face $ {i}$, and points away from the center of the tetrahedron
- $ {V}$ is the volume of the tetrahedron
3. Method 1: Area Vectors
This approach is essentially the one followed here. For any closed shape, the sum of the area vectors is zero:
$ \displaystyle \sum_i \vec{A}_i = 0 \ \ \ \ \ (5)$
This fact is a consequence of the gradient theorem:
$ \displaystyle \sum_i \vec{A}_i = \int_{\partial\Omega} \hat{n}\,dS = \int_\Omega \nabla (1)\,dx = 0 \ \ \ \ \ (6)$
Since the sum is zero, its dot product with any vector $\vec{u}$ will be zero. For starters pick $ {\vec{u} = \vec{A}_1 \times \vec{A}_2}$.
$ \displaystyle \begin{aligned} 0 &= \vec{u}\cdot(\sum_i \vec{A}_i) \\ &= \vec{u}\cdot\vec{A}_1 + \vec{u}\cdot\vec{A}_2 + \vec{u}\cdot\vec{A}_3 + \vec{u}\cdot\vec{A}_4 \end{aligned} \ \ \ \ \ (7)$
The first two terms are $ {\vec{A}_1\times\vec{A}_2\cdot\vec{A}_1}$ and $ {\vec{A}_1\times\vec{A}_2\cdot\vec{A}_2}$ which are zero, so we have that:
$ \displaystyle 0 = \vec{A}_1\times\vec{A}_2\cdot\vec{A}_3 + \vec{A}_1\times\vec{A}_2\cdot\vec{A}_4 \ \ \ \ \ (8)$
Since these two vectors sum to 0, their lengths must be equal:
Repeating this process with $ {\vec{u} = \vec{A}_2\times \vec{A}_3}$ gives
And with $ {\vec{u} = \vec{A}_1\times \vec{A}_3}$:
The order of the vectors in these triple products can be changed arbitrarily without affecting the absolute values, so the right-hand side of (10) is equal to the left-hand side of (9), which is also equal to the right-hand side of (11). Putting together (9)–(11) produces:
Each term in (12) is associated with a vertex – the one whose number is absent. So we have a quantity that is associated with a vertex but whose value does not depend on which vertex one chooses, like the Law of Sines. Now we need to construct a definition for the sine based on this observation. Provisionally, let’s write:
$ \displaystyle \begin{aligned}|\vec{A}_1\cdot (\vec{A}_2\times \vec{A}_3)| &= |\vec{A}_1\cdot (\vec{A}_2\times \vec{A}_4)| \\ &= |\vec{A}_1\cdot( \vec{A}_3\times \vec{A}_4)| \\ &= |\vec{A}_2\cdot( \vec{A}_3\times \vec{A}_4)| = C\frac{|S_i|}{A_i}\end{aligned} \ \ \ \ \ (13)$
where ${S_i}$ is the sine associated with vertex ${i}$ and ${C}$ is some constant to be determined.
The sine should always be in ${[-1,1]}$, and should equal $ {\pm 1}$ when the vectors are all mutually orthogonal. This is accomplished by setting
$ \displaystyle C = A_1 A_2 A_3 A_4 \ \ \ \ \ (14)$
giving
$ \displaystyle S_i = \frac{\vec{A}_p\cdot(\vec{A}_q\times \vec{A}_r)}{A_p A_q A_r} \ \ \ \ \ (15)$
where $ {p,q,r}$ are the numbers from $ {\{1,2,3,4\}}$ that are not equal to $ {i}$. This new sine is called the the polar sine of the area vectors and will be positive or negative depending on the order of the area vectors in the numerator.
4. Method 2: Scalar Areas
The area vectors are not always available or convenient to find, so we would prefer a Law of Sines that uses only the scalar areas. Fortunately this is possible too.
Consider a parallelepiped in $ {d}$ dimensions, with face areas $ {P_1, \dots, P_d}$ (note that the faces are $ {(d-1)}$-dimensional parallelepipeds) and volume $ {P}$. Define the hypersine ${H}$ associated with the common vertex of any ${d}$ faces of the parallelepiped by
$ \displaystyle H = \frac{P^{d-1}}{\prod_{k=1}^{d} P_k} \ \ \ \ \ (16)$
(This section basically repeats the discussion at the page just linked.)
Let ${A_k}$ be the area of a ${(d-1)}$-dimensional simplex built from the edges of face ${k}$, and let ${V}$ be the volume of the ${d}$-dimensional simplex built from the edges of the parallelepiped. In ${d}$ dimensions the volume of a parallelepiped is $d!$ times that of the corresponding simplex, so (16) can be rewritten as:
$ \displaystyle H = \frac{(d!V)^{d-1}}{\prod_{k=1}^{d} (d-1)!A_k} \ \ \ \ \ (17)$
So we have translated the original hypersine definition from being in terms of areas of parallelepipeds to being in terms of areas of simplices, in line with our goal of obtaining a Law of Sines for the tetrahedron whose faces are simplices. Simplifying (17) and labeling the simplex opposite the root vertex as simplex ${0}$:
$ \displaystyle \begin{aligned} \frac{H}{(d-1)!A_0} &= \frac{(d!)^{d-1} V^{d-1}}{((d-1)!)^{d+1} \prod_{k=0}^{d} A_k} \\ &= \left( \frac{d!}{(d-1)!} \right)^{d-1} \frac{V^{d-1}}{((d-1)!)^2} \frac{1}{\prod_{k=0}^{d} A_k} \\ &= \frac{(dV)^{d-1}}{((d-1)!)^2 \prod_{k=0}^{d} A_k} \\ \frac{H}{A_0} &= \frac{(dV)^{d-1}}{((d-1)!) \prod_{k=0}^{d} A_k} \end{aligned} \ \ \ \ \ (18)$
The left-hand side is associated with a specific vertex of the tetrahedron but the right-hand side does not depend on the vertex, so this sine definition has a corresponding Law of Sines.
5. Method 3: Edge Lengths
Face areas in 3D are the direct analog of side lengths in 2D, but one might still expect a Law of Sines involving edge lengths to exist. Pick a vertex $i$ and let $p,q,r$ be the numbers from $\{1,2,3,4\}$ not equal to $i$. Then $ \vec{e}_{ip}, \vec{e}_{iq}, \vec{e}_{ir}$ are the edge vectors emerging from vertex $i$. The volume of the tetrahedron, which won’t depend on the choice of $i$, is:
$ \displaystyle V = |\vec{e}_{ip}\cdot(\vec{e}_{iq}\times \vec{e}_{ir})| \ \ \ \ \ (19)$
Another vertex-independent constant is the product of all the edge lengths of the tetrahedron:
$ \displaystyle E = e_{12} e_{13} e_{14} e_{23} e_{24} e_{34} \ \ \ \ \ (20)$
So a simple Law-of-Sines-like statement would be:
$ \displaystyle \frac{|P_i|}{E_i} = \text{constant} \ \ \ \ \ (21)$
where:
$\displaystyle P_i = \frac{\vec{e}_{ip}\cdot(\vec{e}_{iq}\times \vec{e}_{ir})}{e_{ip} e_{iq} e_{ir}}$
$\displaystyle E_i = e_{pq} e_{qr} e_{pr}$
The sine ${P_i}$ is the triple product of unit edge vectors emerging from vertex $i$, a.k.a. the polar sine of those vectors, and ${E_i}$ is the product of lengths of edges not emerging from vertex $i$.
6. Summary
We ended up with three analogs to the Law of Sines for tetrahedra, each corresponding to a different kind of sine:
Sine Version 1: Polar sine of the area vectors
$ \displaystyle S_i = \frac{\vec{A}_p\cdot (\vec{A}_q\times\vec{A}_r)}{A_p A_q A_r}$
$\displaystyle \frac{|S_1|}{A_1} = \frac{|S_2|}{A_2} = \frac{|S_3|}{A_3} = \frac{|S_4|}{A_4}$
Sine Version 2: Hypersine of the face areas
$\displaystyle H_i = \frac{(d!V)^{d-1}}{(d-1)!\prod_{k=1, k\neq i}^{d} A_k}$
$\displaystyle \frac{H_1}{A_1} = \frac{H_2}{A_2} = \frac{H_3}{A_3} = \frac{H_4}{A_4}$
Sine Version 3: Polar sine of the edge vectors
$\displaystyle P_i = \frac{\vec{e}_{ip}\cdot(\vec{e}_{iq}\times \vec{e}_{ir})}{e_{ip}e_{iq}e_{ir}}$
$\displaystyle \frac{|P_1|}{e_{23}e_{24}e_{34}} = \frac{|P_2|}{e_{13}e_{14}e_{34}} = \frac{|P_3|}{e_{12}e_{14}e_{24}} = \frac{|P_4|}{e_{13}e_{23}e_{23}}$
All the Law-of-Sines analogs involve absolute values because the order of the vectors can change the sign of the sine. This situation does not occur when dealing with triangles because the angles involved in that case are always less than 180 degrees and considered to be positive, so their sines would be positive anyway and no absolute values are necessary.
7. References
- Murray-Lasso, M.A. On a generalization of the law of sines to tetrahedra and simplices of higher dimensions. Ingenieria Investigacion y Tecnologia, Volume 5, No. 3 (2004). Link
- Wikipedia on the polar sine
- Mathworld on the polar sine
- Mathworld on the hypersine