In celebration of the unofficial end of summer (Labor Day in the U.S.), consider a snowpile on a trash bin:

Observe how the shape of the lid (straight edges, rounded corners) seems to propagate upward, and how the sides of each pile are nearly planar with nearly the same slope on each side. Is this a coincidence? Of course not.
The pile is built, of course, by individual flakes landing on flakes that landed before, and if the flakes land on too steep of an incline they will fall off and not contribute the pile that remains after the blizzard. So we should be able to deduce the pile’s eventual shape by considering what must happen for a snowflake to end up perched stationary on the pile:
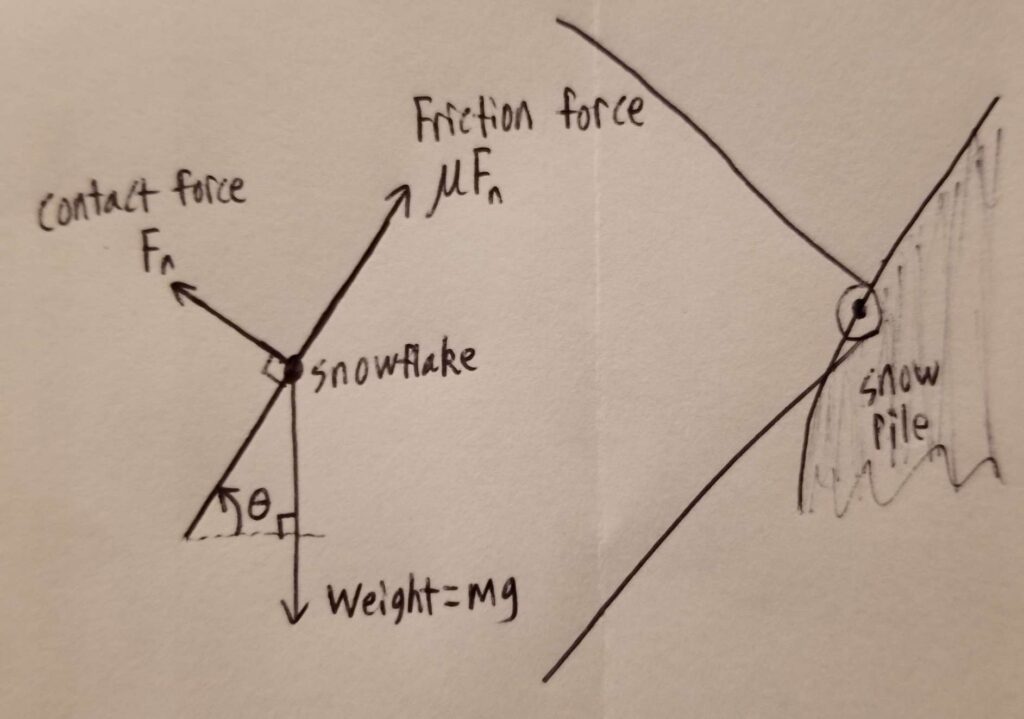
Since the snowflake is not moving, the forces on it must all balance. In particular, the horizontal (perpendicular to gravity) component:
$$\displaystyle -F_n\sin(\theta) + \mu F_n\cos(\theta) \Rightarrow \mu = \tan(\theta)$$
where $\mu$ is the static friction coefficient. In this 2D diagram, $\tan(\theta) = dh/dx$, the gradient of the height $h$, so we have an equation that relates the friction coefficient to the shape of the pile. The 3D equivalent is:
$$\displaystyle |\nabla h| = \mu $$
This is the eikonal equation. Basically it’s saying that at any given point, the steepest gradient in any direction will be as large as friction will permit. If we assume that $\mu$ is constant, the solution will be proportional to the shortest distance to any point on the boundary (the perimeter of the lid). This explains why the shape of the lid affects the shapes of the cross sections moving up the pile. Moreover, since $|\nabla h|$ is constant, it is no surprise that the sides of the pile are (nearly) planar.
The eikonal equation would predict the top of the pile being a sharp point, which clearly is not the case in the picture. This is due to wind which continually shaves off the top of the pile preventing a sharp point from forming.