While a student I often encountered sources claiming something to the effect of “no other special functions have received such detailed treatment […] as the Bessel functions”, which struck me as odd because in the undergraduate differential equations courses I took and taught no mention whatsoever was ever made of them, though the textbook might have a section devoted to the matter. None of the commonly listed applications where they arise relate much to my field, so until deciding to write this post I knew little about them. Now you can know some too.
Bessel’s Differential Equation
The Bessel functions are defined as the solutions $J_\nu$ of the differential equation:
$$\displaystyle x^2 J^{”}_\nu + x J^{\prime}_\nu +(x^2 – \nu^2) J_\nu = 0 $$
where $\nu$ can be any complex number. One can immediately see that the $J_\nu$ are not polynomials, because if $J_\nu$ where a polynomial of degree $d$ then the third term in this equation would have degree $d+2$ and therefore the whole left-hand side could not come out to the zero on the right. Dividing through by $x^2$, one can also see that as $x\to\infty$ the Bessel equation approaches
$$\displaystyle J^{”}_\nu + J_\nu = 0 $$
whose solutions are the sine and cosine functions. Thus the Bessel functions become oscillatory as $x\to\infty$. This fact has ramifications for computing Bessel functions numerically, because although their power series representation
$$\displaystyle J_\nu(x) = \sum_{k=0}^\infty \frac{(-1)^k}{k! \Gamma(k+\nu+1)}\left( \frac{x}{2} \right)^{2k +\nu} $$
converges everywhere, a truncation of it will not capture oscillations that are sufficiently far away from $x=0$. The power series is useful for deriving properties of the $J_\nu$, however, which is fortunate because for most values of $\nu$ the $J_\nu$ cannot be written in terms of elementary functions and must be evaluated numerically. We will see the exceptions later.
The Bessel equation has the form that it does because it arises from the problem of finding eigenvalues of the Laplacian operator in cylindrical coordinates. The eigenvalue problem is:
$$\displaystyle \Delta u + \lambda^2 u = 0$$
and after writing the Laplacian in cylindrical coordinates:
$$\displaystyle u_{rr} + \frac{1}{r} u_r + \frac{1}{r^2} u_{\theta\theta} + \lambda^2 u = 0$$
This problem can be solved by separation of variables. If $u(r,\theta) = R(r)\Theta(\theta)$ then we get after multiplying through by $r^2$:
$$\displaystyle r^2\frac{R^{”}}{R} + r\frac{R^{\prime}}{R} + \lambda^2 r^2 = -\frac{\Theta^{”}}{\Theta} = k^2$$
Since the first expression is real and depends only on $r$ and the second depends only on $\theta$, they must both be a real constant $k^2$. We know it will be positive since otherwise the solution to the $\theta$ equation would become unbounded which is unrealistic. Focusing on the $r$ equation, after some rearrangement we get:
$$\displaystyle r^2 R^{”} + rR^{\prime} + (\lambda^2 r^2 – k^2)R = 0 $$
which after some combining of variables can be seen to be the Bessel differential equation.
Properties of the Bessel Functions
By manipulating the power series, one can show that:
$$\displaystyle \begin{aligned} J_{\nu-1} &= x^{-\nu}\frac{d}{dx} (x^{\nu} J_\nu) = J^{\prime}_\nu + \frac{\nu}{x}J_\nu \\ J_{\nu+1} &= -x^{\nu}\frac{d}{dx} (x^{-\nu}J_\nu) = -J^{\prime}_\nu + \frac{\nu}{x}J_\nu \end{aligned}$$
A little algebra produces the important recurrences:
$$\displaystyle \begin{aligned} J_{\nu-1}+ J_{\nu+1} &= \frac{2\nu}{x}J_\nu \\ J_{\nu-1} – J_{\nu+1} &= 2J^{\prime}_\nu \end{aligned} $$
From the same starting point one can deduce an property of consecutive Bessel functions known as the “interlacing of zeros”. Suppose you have two values $a$ and $b$ for which $J_\nu(a) = J_\nu(b) = 0$, so also $x^\nu J_\nu = x^{-\nu} J_\nu = 0$ there. Then by Rolle’s theorem there exist $x^+$ and $x^-$ such that:
$$\displaystyle \begin{aligned} \frac{d}{dx}\Big|_{x^+} (x^\nu J_\nu(x)) = 0 \\ \frac{d}{dx}\Big|_{x^-} (x^{-\nu} J_\nu(x)) = 0 \end{aligned} $$
From the equations at the top of this section we know that these derivatives are just Bessel functions times $x^{\pm\nu}$, so it follows that $J_{\nu-1}(x^+) = 0 = J_{\nu+1}(x^-)$. Thus between any two zeros of $J_\nu$ there is at least one zero of $J_{\nu+1}$ and at least one zero of $J_{\nu-1}$. Armed with this knowledge we can prove something even stronger. If the two zeros $a$ and $b$ of $J_\nu$ are two consecutive zeros, we know now that they bracket a zero of $J_{\nu-1}$. Maybe they bracket others? But if there were two (or more) zeros of $J_{\nu-1}$ in that range, the same fact we obtained would imply a zero of $J_\nu = J_{\nu-1+1}$ in that range, i.e. the two consecutive zeros we picked at the start are somehow also not consecutive, which is a contradiction. Therefore between any two zeros of $J_\nu$ there is exactly one zero of $J_{\nu-1}$ and exactly one zero of $J_{\nu+1}$.
That argument assumes that there are any zeros to pick from in the first place, which is easy to believe by looking at the graphs of the Bessel functions with $\nu = 0,1,2,3,4$:
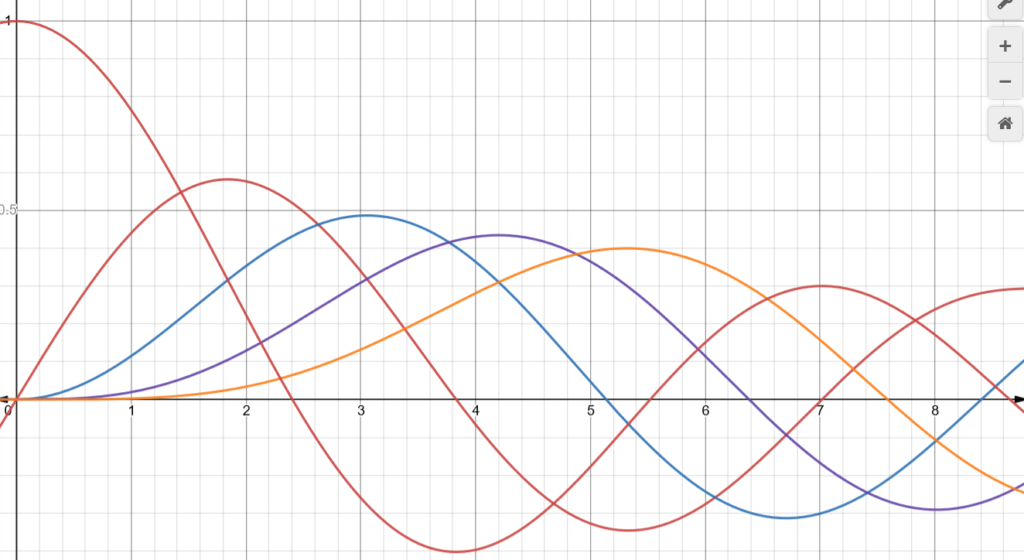
But we are talking about any possible value of $\nu$. In fact, as one would expect from the limiting oscillatory behavior noted earlier, the Bessel functions have infinitely many zeros.
Hearing the Shape of a Drum
The zeros of Bessel functions arise in the context of boundary value problems on circular regions. For example, consider a circular drumhead clamped tight around its circumference. The displacement $u$ from the motionless position of a point on the drumhead satisfies the wave equation:
$$\displaystyle u_{tt} = c^2 \Delta u$$
which, you’ll notice, involves the Laplacian. This equation can be solved by a separation of variables approach similar to the one above, so for brevity I will skip that process and say that at the end, you get for the radial factor $R$:
$$\displaystyle R^{”} +\frac{1}{s} R^{\prime} + R(s) = 0 $$
which is a Bessel equation with $\nu = 0$ so $R(s) = J_0(s)$. $s = \lambda r/c$ is a variable related to the distance $r$ from the center of the drum, the speed $c$ at which disturbances travel along the drumhead, and the frequency of vibration $\lambda$. Because the drumhead is clamped at the circumference, which let’s say corresponds to $r = r_c$, the displacement there must be zero. That is, $J_0(\lambda r_c/c) = 0$. Since $r_c$ comes from the shape of the drum, which is constant, and $c$ comes from the material properties of the drumhead, which are also constant, this constraint of zero motion at the circumference translates into a constraint on the vibration frequency $\lambda$. The only frequencies at which the drumhead can vibrate are those that coincide with a zero of the Bessel function $J_0$. In reality, hitting a drum causes vibrations at all of these possible frequencies simultaneously.
This fact has a musical consequence. The available zeros of $J_0$ are not equally spaced, though they are not far off from being so. This means that the frequencies of vibration for a drum are not all multiples of each other (harmonics) as is the case for a plucked string. Hence a drum and a string bass tuned to produce the same fundamental frequency will still produce different sounds, because the higher frequencies produced by the instruments will differ.
Bessel Functions of Half-Integer Order
As mentioned previously, only for certain values of $\nu$ can the Bessel functions be written in terms of familiar functions. To see this, we start with the power series and set $\nu = \frac{1}{2}$:
$$\displaystyle J_{1/2}(x) = \sum_{k=0}^\infty \frac{(-1)^k}{k!\Gamma(k+\frac12 + 1)} \left( \frac{x}{2} \right)^{2k+1/2} $$
Pulling out some factors and using the property of the gamma function that $\Gamma(a+1) = a\Gamma(a)$:
$$\displaystyle J_{1/2}(x)= \left( \frac{x}{2}\right)^{-\frac12} \frac{1}{\Gamma(\frac12)} \sum_{k=0}^\infty \frac{(-1)^k}{k! \frac12\frac32\dots\frac{2k+1}{2}} \left( \frac{x}{2} \right)^{2k+1} $$
The power of $x/2$ provides $2k+1$ factors of $2$ to be distributed over the denominator, which is enough to make it into a simple factorial:
$$\displaystyle J_{1/2}(x) = \left( \frac{x}{2}\right)^{-\frac12} \frac{1}{\sqrt{\pi}} \sum_{k=0}^\infty \frac{(-1)^k}{(2k+1)!} x^{2k+1} $$
using also the fact that $\Gamma(1/2)= \sqrt{\pi}$. You may recognize this new power series as that for $sin(x)$, so we have arrived at:
$$\displaystyle J_{1/2}(x) = \sqrt{\frac{2}{\pi x}}\sin(x) $$
A similar process shows that
$$\displaystyle J_{-1/2}(x) = \sqrt{\frac{2}{\pi x}}\cos(x) $$
Using the recurrence relations previously derived, one can obtain any of $J_{\pm 3/2}, J_{\pm 5/2}, J_{\pm 7/2}$ etc. using these formulas for $J_{\pm 1/2}$. There is also a general formula for these functions:
$$\displaystyle J_{n+1/2}(x) = \sqrt{\frac{2}{\pi}} x^{n+1/2} \left( \frac{1}{x}\frac{d}{dx} \right)^n \frac{\sin(x)}{x} $$
Other Kinds of Bessel Functions
So far I have referred to $J_\nu$ simply as “Bessel functions” for convenience, but they are more properly called Bessel functions of the first kind. If $\nu$ is not an integer, then $J_\nu$ and $J_{-\nu}$ are linearly independent and thus form a basis for all solutions of the Bessel differential equation. However if $\nu$ is an integer, then $J_\nu$ and $J_{-\nu}$ are linearly dependent so an additional solution to the differential equation is required for a complete basis. This additional solution is the Bessel function of the second kind, commonly denoted $Y_\nu$:
$$\displaystyle Y_{\nu} = \frac{J_{\nu}\cos(\nu\pi) – J_{-\nu}}{\sin(\nu\pi)} $$
This definition works for non-integer $\nu$, but for integer $\nu$ the denominator becomes zero so the definition is the limit as $\nu$ approaches the integer. Bessel functions of the first and second kinds combine to form those of the third kind, also known as Hankel functions:
$$\displaystyle \begin{aligned} H_{\nu}^{(1)} &= J_\nu + iY_\nu \\ H_{\nu}^{(2)} &= J_\nu – iY_\nu \end{aligned}$$
The Hankel functions are analogous to the complex exponential. For the differential equation $u^{”} + u = 0$ one usually speaks of the solutions being $\sin(x)$ and $\cos(x)$ since those functions are real. However it is also valid to take $e^{ix}$ and $e^{-ix}$ as the solutions since they each satisfy the equation. But note that $e^{ix} = \cos(x) + i\sin(x)$, so we’re merely combining the two real solutions into a complex one, not getting any fundamentally new solutions. In the context of Bessel functions the original equation is different, but the Bessel functions of first, second, and third kind play the roles of $\cos(x)$, $\sin(x)$, and $e^{ix}$ respectively.
Wrapping Up
The motivation for this post was to familiarize myself with Bessel functions so that I would recognize them when I saw one, and would understand some of their key properties. Hopefully it has helped you do that too. But there is much more material out there on the subject. Here is some of it:
- A primer that gives some properties and puts Bessel functions in the context of Sturm-Liouville problems. Incidentally this was written by a former professor of mine.
- An appendix from a textbook that goes into some depth and includes connections with the Airy functions. Note that Equation B.10 has a typo.